Homework 4: Prediction vs Inference

Here are the formulas in textbooks and from our slides when all 5 assumptions are satisfied under simple linear regression:

• \[\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}\]
• \[\hat{\beta}_1 = Corr_{x, y}\frac{SD_y}{SD_x}\]
• \[SE(\hat{\beta}_1|X) = \sqrt{\frac{\sigma^2}{\sum (x_i - \bar{x})^2}}\]
• \[SE(\hat{\beta}_0|X) = \sqrt{\sigma^2\left[\frac{1}{n} + \frac{\bar{x}^2}{\sum (x_i - \bar{x})^2}\right]}\]
• \[\hat{\sigma}^2 = \frac{1}{n-2}\sum (y_i - \hat{y}_i)^2\]
• \[\frac{\hat{\beta}_1}{\hat{SE}(\hat{\beta}_1|X)} \sim t_{df=n-2}\]
• \[\frac{\hat{\beta}_0}{\hat{SE}(\hat{\beta}_0|X)} \sim t_{df=n-2}\]

Note that:

\(\hat{SE}(\hat{\beta}_1 \vert X)\) differs from \(SE(\hat{\beta}_1 \vert X)\) becase it estimates \(\sigma^2\) with \(\hat{\sigma}^2\)

Q1 - Verifying calculations from summary.lm()

Please create a matrix or data frame called summ_tab using the formulas above that matches the output from the coefficients attribute under summary.lm() You may use basic functions like pt(), mean(), sd(), corr(), sum(), /, etc

Please generate your own random dataset to demonstrate this.

Hint: df stands for degrees of freedom.

Q2 - different ways to generate data

Please first generate data using the following code:

n <- 50
x <- rnorm(n)
z <- runif(n)
w <- rexp(n)
indep_vars <- cbind(x, z, w)

errors <- rnorm(n, sd=10)
betas <- c(1, 2, 3, 4)
y <- betas[1] + betas[2] * x + betas[3] * z + betas[4] * w + errors
# The following will produce an error
should_be_y <- indep_vars %*% betas + errors

The %*% symbol is how we tell R to perform matrix multiplication. The last line above should produce an error. Please modify indep_vars such that y and should_be_y are almost identical (within machine precision). Be sure to demonstrate that the two variables, after your fix, are almost identical.

FYI, R implicitly treats vectors as matrices as n by 1 matrices when doing matrix operations.

Q3 - Paper Trustworthiness (long)

You’ll need the CSV file on Ed Resources titled “trustworthiness.csv”. This is shared by the authors of Trustworthiness of Crowds is gleaned in half a second and processed by your instructor.

You do not need to read the whole paper to do this problem but the lead author will speak at our class on 11/8/2023.

We will focus on the 3rd study, where people role-play as investors for individual business associates or groups of business associates. They could invest any amount between $0.00 and $1.00 in $0.25 increments. The investment will triple but the amount returned to the investor will depend on the business associates. The business associates’ faces were exposed only for 500ms to the investors. There were 50 photos in each categories: individual face (a single face was shown), an ensemble of faces (ensemble which includes the single face), and an individual’s face surrounded by other members (highlighted).

• What is the dimension of the data?
• How many unique subjID are in the data?
• What are the possible values in Response.bordered ? (This is the response from the highlighted face surrounded by an ensemble)
• How many missing values exist in the gender variable?
• At the beginning of discussing Study 3, the authors shared some demographics of the participants.
  • If these demographics are different from the population, e.g. 50/50 male/female, what can we conclude?
  • If these demographics are close to the population, e.g. 50/50 male/female, what can we conclude?
  • Please show your code that reproduces the demographic distributions for Study 3 in the paper
• Pick a random image (a single unique value from all the possible pic_id), then plot the highlighted response (Response.bordered) vs the single face response (Response.single). Please state whether you believe (the following are graded by effort):
  • linearity exists between the two variables
  • whether the scatter plot is homoscedastic
  • whether you believe the responses are independent from one another?

Q4 - confidence intervals for the line from different bootstraps

Use the file hw4_scatter.csv, please reproduce the following plot:

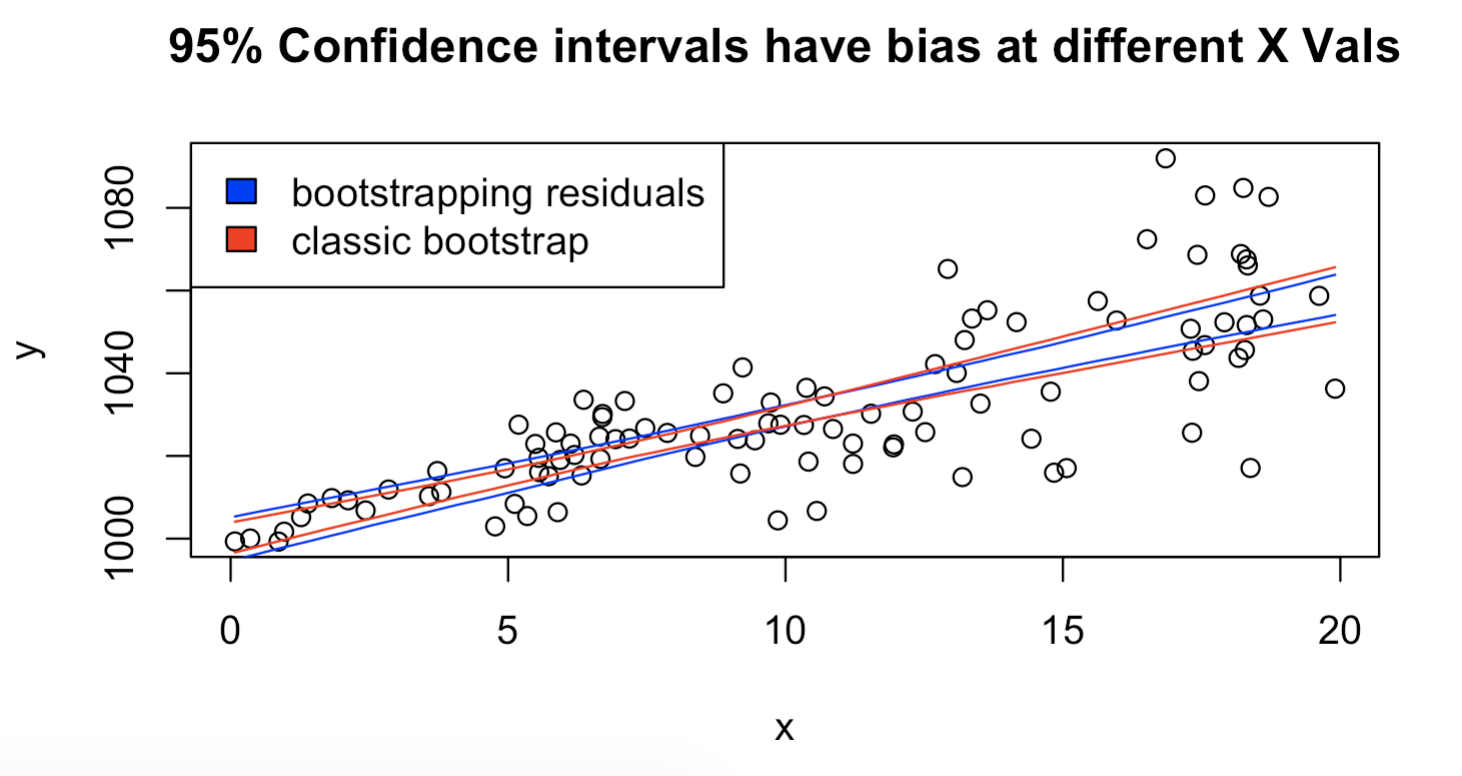
Hint:

• Each regression fitted from a bootstrap will produce a value at any “X” location. The width of the inner 95% of these fitted values should be a good estimate for the width of your confidence interval!

Q5 - intuition practice

• Continuing from Q4, If we used predict.lm(..., interval="confidence"), would its results align better with the classic bootstrap or bootstrapping the residuals?
• Which method is more “correct”, the classic bootstrap or bootstrapping the residuals? Explain your choice with at most 2 sentences.

Q6 - Prediction Intervals

First generate your data following the process below:

set.seed(100)
n <- 50
x_range <- 1:20
beta0 <- -5
beta1 <- 1.2
x <- sample(x_range, n, replace=TRUE)
y <- beta0 + beta1 * x + rnorm(n)

Do not overwrite your original x, y data pairs.

• Plot the 80% confidence interval and prediction interval on the scatter plot of x and y (hint: predict.lm()). The range of x values should be all the integers from 1 through 20.
• Generate 1000 new data pairs, report the percentage of them are within your prediction interval?

Q7 - Prediction or inference

For each of the following, please state whether we should care about the prediction interval or the confidence interval for the regression line, no need to explain your choice.

• For several similar startups, you have their user engagement data (e.g. page views) and how much they spent on marketing, you’re curious about how much engagement your startup (in the same field) will get if you spend X dollars. Should you use a prediction interval or confidence interval?
• You have data on a specific spring between the weight placed on it vs the length it stretched (the length is measured by eye-balling, i.e. noisy). You want to guess the length of this particular spring if you give it weights you have not measured before, should you compute the confidence interval or the prediction interval for this problem?
• The government can learn the relationship between investment in education vs poverty levels to make county-level policies that would affect many households, should they compute the confidence interval or the prediction interval?

Q8 - How categorical values are turned into numbers and handled in regression

Run the following code

n <- 50
cat_variable <- c('A', 'B', 'C')
group <- factor(sample(cat_variable, n, replace=TRUE), levels=cat_variable)
y <- rnorm(n)

X <- model.matrix(~group)
mod <- lm(y ~ group)
mod2 <- lm(y ~ X)

• Examine at the first few rows of X and explain the relationship between X and group using no more than 4 sentences.
• mod2 has a coefficient listed as NA, how can we change the code above such that this doesn’t happen? Please explain why this happens using at most 2 sentences (we’re looking for one keyword).
• Please verify or disprove that mod and mod2 are “the same” from a statistical perspective? Statistical here means attributes, artifacts, or behavior from the model.